Line groups: Symmetry of Polymers and nanotubes Polymer with screw axis arranged monomers
Symmetries of polymers are described by the line groups. These groups are derived at the beginning of 20. century, but only in 1976 our colleagues I. Bozovic (Ph. D. Thesis,1975), M. Vujicic and F. Herbut made systematic construction of the commensurate ones (in terms of generalized semidirect product) together with their irreducible representations in 1977 and 1979.

Factorization of these groups on the cyclic factors by M. Damnjanovic with introduction of helical quantum numbers and magnetic line groups (Ph. D. Thesis, 1981) enabled stratification of Euclid space by I. Milosevic (together with phonon assignation and proof of Jahn-Teller teorem, M. Sc. Thesis,1993), and traced the path for symbolic computing with groups within framework of modified group projector technique (Ph.D.Thesis,1996).

Research on the line groups continued, enlightening a number of properties of these groups: Molien functions for the line groups have been calculated T. Vukovic (B.Sc.Thesis,1997) providing complete determination of the most general forms of the invariant potentials for all quasi-1D systems (applied in analysis of commensurate and incommensurate phase transition in polymers and 3D crystals). Diffraction patterns, double line groups, elementary band representations are only few of the results of NanoLab members (S. Dmitrovic, N. Lazic) on these groups. The main results are summarized in the specialized monography.
For each of 13 family of the line groups different factorizations in the form L=ZP are given (Z is infinite cyclic group of generalized translations - pure translations T, screw axis Trq or glide plane Tc, and P is axial point group). The maximal first family subgroup and isogonal point group PI, are presented (n is the order of the principle rotational axis of P, andq of PI). Here, Tcd denotes the glide plain bisecting the angle between vertical mirror planes in P. For the groups of the families 1 and 5, q is multiple of n (p from the international symbol is function of n, q and r)

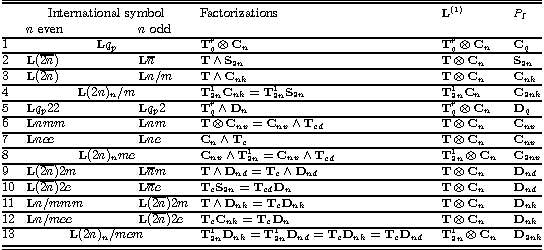The line group symmetry is basis for the research of diverse physical properties of nanotubes polymers (phase transitions, selection rules, physical tensors). Rolling up relation to the layer groups enabled to find the line group symmetry of various nanotubes.

The computer program POLSym® enables the efficient analysis of the polymer properties, implementing their symmetry through the modified group projector technique. Such studies are easily performed even for complex polymers as the DNA macromolecule.


References